maths problem (involving spheres)
-
there are two water tanks providing water: a primary water tank, which is a sphere with a 4.5 metre radius, and a much larger backup water tank. the primary water tank is empty.
the primary water tank is to be filled up such that the water is exactly 6.5 metres deep at the center. If one bucket of water holds exactly 10 litres, how many bucketfuls of water are required to fill the tank to the required depth? Round up to the nearest whole number. -
You may be missing some information there because your question has nothing to do with the back up tank. I suspect your question may have something to do with similar figures.
Otherwise, This is a very difficult problem. You may want to read up this: http://mathcentral.uregina.ca/qq/database/QQ.09.99/partridge1.html
which explains how the formula of sphere is derived. The same principle may well be applied to calculate the vol of 1/4 full sphere. 6.5m filled sphere. (But i also dunno) -
haha the larger backup tank is just a place whereby water is being fetched from.. nothing else. ^_^Originally posted by Gasfene:You may be missing some information there because your question has nothing to do with the back up tank. I suspect your question may have something to do with similar figures.
Otherwise, This is a very difficult problem. You may want to read up this: http://mathcentral.uregina.ca/qq/database/QQ.09.99/partridge1.html
which explains how the formula of sphere is derived. The same principle may well be applied to calculate the vol of 1/4 full sphere. 6.5m filled sphere. (But i also dunno) -
I've thought of a method but I dun know whether it works or not.
You consider the top part of the sphere that is not filled by water. Observe that in 2-dimensional drawing, it's cutting off the top part of a circle.
Now consider an x-y axis graph, line up this top part such that the straight line coincides with the y axis. I think if you were to reflect this graph along the y axis, you'll get an ellipse and thus you can determine the actual equation of this curve.
Now if I recall, you can integrate this curve from x = 0 to x = 3.5 and consider a 360 degrees rotation along the x-axis to get the volume of this cut-off part. But exact method escapes me at the moment.
Thus, you can determine the full sphere volume and the volume you want is just the full volume - volume of top part, then just divide by 10 to get the answer.
Hmmm....is that it?
-
something i tot of
although i got some inspiration from coolmyth ^_^
before everything, the volume of sphere = 4/3*pi*(4.5^3)= 381.7m^3
6.5 metres filled meaning 2.5 metres is empty
ok think of a sphere and then u cut away (the diameter)9 - 2.5 metres at each side... meaning the top, the bottom, the front and back and both the left and right side. u will get a cube with each sides being 4m.
the volume of the cube is thus 4^3 = 64m^3
therefore, the total volume being cut off = 381.7 - 64 = 317.7m^3
since we cut off 6 parts, the volume of each part = 317.7 / 6 = 52.95m^3
therefore, the volume of sphere at the height of water being 6.5m = 381.7 – 52.95 = 328.75m^3
since 1 pail can fetch 10 litres of water = 10x 1000cm^3 = 10000x10^-6 m^3
the total number of pails of water needed = 328.75 / 10000x10^-6 = 32875 pails of water.
edit: haha i think the answer is wrong... i was wrong at the cutting part... coz for a sphere you can not get 6 equal parts... lol its hard to explain in words but the solution is wrong anyway. -
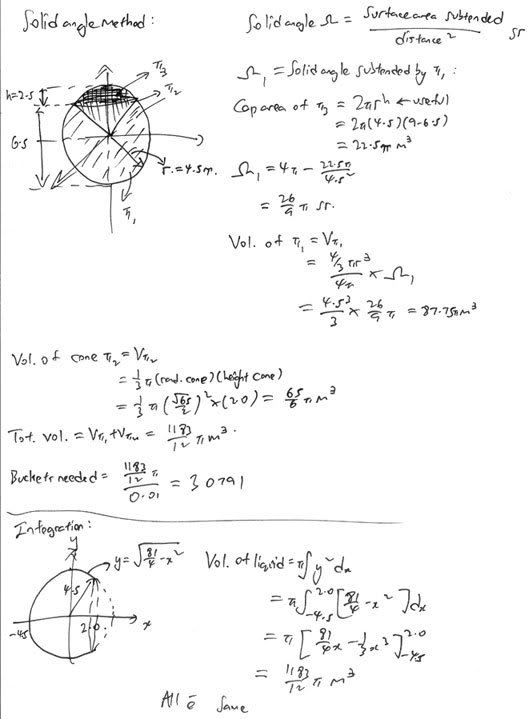
1st method if u dunoe integration -
Nice.

I can get the integration method. First one, the handwriting I can't understand that well.
-
no need any bucketful. i use hose
